6DOF/it

Linapod 6DOF

Release status: Concept

Description	Cinematica a sei gradi di libertà per Linapod sviluppata dall'ISW.
License	CC-BY-SA
Author	User:Bruno.laterza
Contributors
Based-on	[[]]
Categories	Principles
CAD Models
External Link

Per poter gestire un attuatore che sia libero di assumere una qualsiasi posizine (sia <math>(x,y,z)</math> che nelle rotazioni <math> (\alpha, \beta, \gamma)</math>) serve una macchina che gestisca almeno 5 gradi di libertà; di seguito si esporranno i calcoli per poter gestire la cinematica inversa di Linapod, una macchina a sei gradi di libertà, sviluppata dall'ISW.

Si introdurrà il funzionamento della cinematica, presupponendo che le catene cinematiche siano funzionanti.

Con questi calcoli si vuole realizzare una macchia con sei gradi di libertà, in grado di muovere l'utensile in tutte le posizioni <math>(x,y,z)</math> e in tutte le rotazioni <math> (\alpha, \beta, \gamma)</math>.

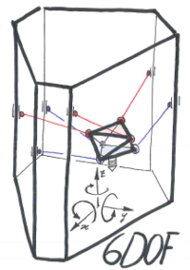
Linapod

Linapod è un robot a cinematica parallela con sei gradi di libertà. Per poterli gestire si usano sei attuatori lineari prismatici.

Le sei catene cinematiche sono composte da tre giunti P-S-S (prismatico sferico sferico). il giunto lineare P è motorizzato, e tramite le posizioni dei sei giunti P si determinerà la posizione nei 6 gradi del'End-Effector.

catena cinematica parallela P-S-S

---

Definizioni

si definiranno due sistemi di riferimento, Base <math>{\left \{ A \right \}}</math> e End-Effector <math>{\left \{ EE \right \}}</math>. Inoltre dove necessario i punti avranno un prefisso che indicherà a che sistema di riferimento al si appoggiano (messo come apice sinistro).

Base

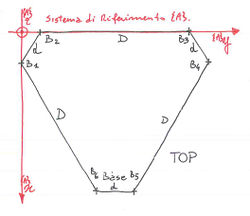
definisco il sistema di riferimeto della base e che indicherò con <math>{\left \{ A \right \}}</math> come da figura.

Base top in <math>{\left \{ A \right \}}</math>

Base side in <math>{\left \{ A \right \}}</math>

Punti <math> ^{\left \{ A \right \}}B_i , i=1..6 </math> solidali al <math>{\left \{ A \right \}}</math> in coordinate omogenee.

<math> ^{\left \{ A \right \}}B_1:\left(\frac{\sqrt{3}d}{2},0,0,1 \right)</math>;

<math> ^{\left \{ A \right \}}B_2:\left(0,\frac{d}{2},0,1 \right)</math>;

<math> ^{\left \{ A \right \}}B_3:\left(0,D + \frac{d}{2},0,1 \right)</math>;

<math> ^{\left \{ A \right \}}B_4:\left(\frac{\sqrt{3}d}{2},D + d,0,1 \right)</math>;

<math> ^{\left \{ A \right \}}B_5:\left(\frac{\sqrt{3}(D+d)}{2},\frac{D}{2} + d,0,1 \right)</math>;

<math> ^{\left \{ A \right \}}B_5:\left(\frac{\sqrt{3}(D+d)}{2},\frac{D}{2},0,1 \right)</math>;

i <math> ^{\left \{ A \right \}}B_i</math> sono i sei assi su cui appoggiano i giunti prismatici.

Punti <math> ^{\left \{ A \right \}}P_i , i=1..6 </math> solidali al <math>{\left \{ A \right \}}</math> in coordinate omogenee rappresentano i sei punti comandati dagli attuatori, e i <math> c_i </math> rappresentano le variabili da comandare con gli attuatori.

<math> ^{\left \{ A \right \}}P_1:\left(\frac{\sqrt{3}d}{2},0,c_1,1 \right)</math>;

<math> ^{\left \{ A \right \}}P_2:\left(0,\frac{d}{2},c_2,1 \right)</math>;

<math> ^{\left \{ A \right \}}P_3:\left(0,D + \frac{d}{2},c_3,1 \right)</math>;

<math> ^{\left \{ A \right \}}P_4:\left(\frac{\sqrt{3}d}{2},D + d,c_4,1 \right)</math>;

<math> ^{\left \{ A \right \}}P_5:\left(\frac{\sqrt{3}(D+d)}{2},\frac{D}{2} + d,c_5,1 \right)</math>;

<math> ^{\left \{ A \right \}}P_6:\left(\frac{\sqrt{3}(D+d)}{2},\frac{D}{2},c_6,1 \right)</math>;

inoltre i sei braccetti che congiungono l'End-Effector sono di due misure <math> B </math> e <math> b </math>.

---

End-Effector

Base top in <math>{\left \{ A \right \}}</math>

Base side in <math>{\left \{ A \right \}}</math>

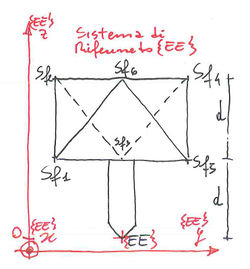
definiamo, come in figura, i sei punti <math> Sf_i , i=1..6 </math> dei giunti sferici dell'end effector in coordinate omogenee riferiti al sistema di riferimento <math>{\left \{ EE \right \}}</math>. Il sistema di riferimento <math>{\left \{ EE \right \}}</math> è solidale all'End-Effector e l'origine coincide con la punta dell'attuatore.

<math> ^{\left \{ EE \right \}}Sf_1:\left(\frac{d}{2\sqrt{3}},-\frac{d}{2},d,1 \right)</math>;

<math> ^{\left \{ EE \right \}}Sf_2:\left(-\frac{d}{2\sqrt{3}},-\frac{d}{2},2 d,1 \right)</math>;

<math> ^{\left \{ EE \right \}}Sf_3:\left(-\frac{d}{\sqrt{3}},0,d,1 \right)</math>;

<math> ^{\left \{ EE \right \}}Sf_4:\left(-\frac{d}{2\sqrt{3}},\frac{d}{2},2 d,1 \right)</math>;

<math> ^{\left \{ EE \right \}}Sf_5:\left(\frac{d}{2\sqrt{3}},\frac{d}{2},d,1 \right)</math>;

<math> ^{\left \{ EE \right \}}Sf_6:\left(\frac{d}{\sqrt{3}},0,2 d,1 \right)</math>;

Matrice di rototraslazionezione Omogenea

Matrice:

definiamo la matrice di rotazione del S.d.r. <math>{\left \{ EE \right \}}</math> (End Effector) rispetto <math>{\left \{ A \right \}}</math> (Base). tutti i conti sono fatti in coordinate omogenee.

nel definirla si usa rotazione con angoli RPY rispetto alla terna fissa <math>{\left \{ A \right \}}</math>} definisco le due SOLE rotazioni:

- Prima intorno all'asse 'x' di rotazione <math> \gamma</math>

- Seconda intorno all'asse 'y' di rotazione <math> \beta</math>

inteso verso antiorario positivo.

<math> ^{\left \{ A \right \}}T_{\left \{ EE \right \}} : \begin{bmatrix} \cos\beta & \sin\beta \sin\gamma & \sin\beta \cos\gamma & t_1 \\ 0 & \cos\gamma & -\sin\gamma & t_2 \\ -\sin\beta & \cos\beta \sin\gamma & \cos\beta \cos\gamma & t_3 \\ 0 & 0 & 0 & 1 \end{bmatrix} </math>

questa matrice applicata ai punti <math>^{\left \{ EE \right \}}Sf_i , i=1..0</math> me li riferisce al sistema di riferimento <math>{\left \{ A \right \}}</math>}. facendo così ho i punti dell'End-Effector roto-traslati riferiti al <math>{\left \{ A \right \}}</math>} e facili da usare per calcolare la cinematica inversa della macchina.

Punti rototraslati

applico la matrice ai punti:

<math> ^{\left \{ A \right \}}Sf_i := ^{\left \{ A \right \}}T_{\left \{ EE \right \}} \cdot ^{\left \{ EE \right \}}Sf_i </math>

<math> ^{\left \{ A \right \}}Sf_i := \begin{bmatrix} \cos\beta & \sin\beta \sin\gamma & \sin\beta \cos\gamma & t_1 \\ 0 & \cos\gamma & -\sin\gamma & t_2 \\ -\sin\beta & \cos\beta \sin\gamma & \cos\beta \cos\gamma & t_3 \\ 0 & 0 & 0 & 1 \end{bmatrix} \cdot ^{\left \{ EE \right \}}Sf_i </math>

quindi i sei punti riferiti ad <math> {\left \{ A \right \}} </math> risultano:

<math> ^{\left \{ A \right \}}Sf_1 = \begin{pmatrix}t_1-\frac{\mathrm{sin}\left( \beta\right) \cdot d\cdot \mathrm{sin}\left( \gamma\right) }{2}+\mathrm{sin}\left( \beta\right) \cdot d\cdot \mathrm{cos}\left( \gamma\right) +\frac{\mathrm{cos}\left( \beta\right) \cdot d}{2\cdot \sqrt{3}}\cr t_2-d\cdot \mathrm{sin}\left( \gamma\right) -\frac{d\cdot \mathrm{cos}\left( \gamma\right) }{2}\cr t_3-\frac{\mathrm{cos}\left( \beta\right) \cdot d\cdot \mathrm{sin}\left( \gamma\right) }{2}+\mathrm{cos}\left( \beta\right) \cdot d\cdot \mathrm{cos}\left( \gamma\right) -\frac{\mathrm{sin}\left( \beta\right) \cdot d}{2\cdot \sqrt{3}}\cr 1\end{pmatrix} </math>;

<math> ^{\left \{ A \right \}}Sf_2 = \begin{pmatrix}t_1-\frac{\mathrm{sin}\left( \beta\right) \cdot d\cdot \mathrm{sin}\left( \gamma\right) }{2}+2\cdot \mathrm{sin}\left( \beta\right) \cdot d\cdot \mathrm{cos}\left( \gamma\right) -\frac{\mathrm{cos}\left( \beta\right) \cdot d}{2\cdot \sqrt{3}}\cr t_2-2\cdot d\cdot \mathrm{sin}\left( \gamma\right) -\frac{d\cdot \mathrm{cos}\left( \gamma\right) }{2}\cr t_3-\frac{\mathrm{cos}\left( \beta\right) \cdot d\cdot \mathrm{sin}\left( \gamma\right) }{2}+2\cdot \mathrm{cos}\left( \beta\right) \cdot d\cdot \mathrm{cos}\left( \gamma\right) +\frac{\mathrm{sin}\left( \beta\right) \cdot d}{2\cdot \sqrt{3}}\cr 1\end{pmatrix} </math>;

<math> ^{\left \{ A \right \}}Sf_3 = \begin{pmatrix}t_1+\mathrm{sin}\left( \beta\right) \cdot d\cdot \mathrm{cos}\left( \gamma\right) -\frac{\mathrm{cos}\left( \beta\right) \cdot d}{\sqrt{3}}\cr t_2-d\cdot \mathrm{sin}\left( \gamma\right) \cr t_3+\mathrm{cos}\left( \beta\right) \cdot d\cdot \mathrm{cos}\left( \gamma\right) +\frac{\mathrm{sin}\left( \beta\right) \cdot d}{\sqrt{3}}\cr 1\end{pmatrix} </math>;

<math> ^{\left \{ A \right \}}Sf_4 = \begin{pmatrix}t_1+\frac{\mathrm{sin}\left( \beta\right) \cdot d\cdot \mathrm{sin}\left( \gamma\right) }{2}+2\cdot \mathrm{sin}\left( \beta\right) \cdot d\cdot \mathrm{cos}\left( \gamma\right) -\frac{\mathrm{cos}\left( \beta\right) \cdot d}{2\cdot \sqrt{3}}\cr t_2-2\cdot d\cdot \mathrm{sin}\left( \gamma\right) +\frac{d\cdot \mathrm{cos}\left( \gamma\right) }{2}\cr t_3+\frac{\mathrm{cos}\left( \beta\right) \cdot d\cdot \mathrm{sin}\left( \gamma\right) }{2}+2\cdot \mathrm{cos}\left( \beta\right) \cdot d\cdot \mathrm{cos}\left( \gamma\right) +\frac{\mathrm{sin}\left( \beta\right) \cdot d}{2\cdot \sqrt{3}}\cr 1\end{pmatrix} </math>;

<math> ^{\left \{ A \right \}}Sf_5 = \begin{pmatrix}t_1+\frac{\mathrm{sin}\left( \beta\right) \cdot d\cdot \mathrm{sin}\left( \gamma\right) }{2}+\mathrm{sin}\left( \beta\right) \cdot d\cdot \mathrm{cos}\left( \gamma\right) +\frac{\mathrm{cos}\left( \beta\right) \cdot d}{2\cdot \sqrt{3}}\cr t_2-d\cdot \mathrm{sin}\left( \gamma\right) +\frac{d\cdot \mathrm{cos}\left( \gamma\right) }{2}\cr t_3+\frac{\mathrm{cos}\left( \beta\right) \cdot d\cdot \mathrm{sin}\left( \gamma\right) }{2}+\mathrm{cos}\left( \beta\right) \cdot d\cdot \mathrm{cos}\left( \gamma\right) -\frac{\mathrm{sin}\left( \beta\right) \cdot d}{2\cdot \sqrt{3}}\cr 1\end{pmatrix} </math>;

<math> ^{\left \{ A \right \}}Sf_6 = \begin{pmatrix}t_1+2\cdot \mathrm{sin}\left( \beta\right) \cdot d\cdot \mathrm{cos}\left( \gamma\right) +\frac{\mathrm{cos}\left( \beta\right) \cdot d}{\sqrt{3}}\cr t_2-2\cdot d\cdot \mathrm{sin}\left( \gamma\right) \cr t_3+2\cdot \mathrm{cos}\left( \beta\right) \cdot d\cdot \mathrm{cos}\left( \gamma\right) -\frac{\mathrm{sin}\left( \beta\right) \cdot d}{\sqrt{3}}\cr 1\end{pmatrix} </math>;

Risoluzione cinematica inversa

Definizione Sfere

adesso che si hanno definito tutti i punti in <math> {\left \{ A \right \}} </math> si risolverà vincolando i punti <math> ^{\left \{ A \right \}}Sf_i </math> alle sfere di centro <math> ^{\left \{ A \right \}}P_i </math> e di raggio opportuno: <math> B </math> o <math> b </math>.

quindi:

<math> ^{\left \{ A \right \}}S_i : = {{\left( x - ^{\left \{ A \right \}}P_i(x) \right) }^{2}} + {{\left( y - ^{\left \{ A \right \}}P_i(y) \right) }^{2}} + {{\left( z - ^{\left \{ A \right \}}P_i(z) \right) }^{2}} - b^2 </math>

che facendo le opportune sostituzioni si hanno:

<math> ^{\left \{ A \right \}}S_1 : = {{\left( z-c_1\right) }^{2}}+{{y}^{2}}+{{\left( x-\frac{\sqrt{3}\cdot d}{2}\right) }^{2}}-{{b}^{2}} </math>

<math> ^{\left \{ A \right \}}S_2 : = -{{B}^{2}}+{{\left( z-c_2\right) }^{2}}+{{\left( y-\frac{d}{2}\right) }^{2}}+{{x}^{2}} </math>

<math> ^{\left \{ A \right \}}S_3 : = {{\left( -D+y-\frac{d}{2}\right) }^{2}}+{{\left( z-c_3\right) }^{2}}+{{x}^{2}}-{{b}^{2}} </math>

<math> ^{\left \{ A \right \}}S_4 : = {{\left( -D+y-d\right) }^{2}}-{{B}^{2}}+{{\left( z-c_4\right) }^{2}}+{{\left( x-\frac{\sqrt{3}\cdot d}{2}\right) }^{2}} </math>

<math> ^{\left \{ A \right \}}S_5 : = {{\left( x-\frac{\sqrt{3}\cdot \left( D+d\right) }{2}\right) }^{2}}+{{\left( -\frac{D}{2}+y-d\right) }^{2}}+{{\left( z-c_5\right) }^{2}}-{{b}^{2}} </math>

<math> ^{\left \{ A \right \}}S_6 : = {{\left( x-\frac{\sqrt{3}\cdot \left( D+d\right) }{2}\right) }^{2}}+{{\left( y-\frac{D}{2}\right) }^{2}}-{{B}^{2}}+{{\left( z-c_6\right) }^{2}} </math>

Vincolare i punti dell'End-Effector alle sfere

Le sfere definite come sopra sono l'insieme di tutti i punti che possono essere presi dai <math> ^{\left \{ A \right \}}Sf_i </math> per ogni i=1..6. inoltre le sfere sono definite da un unica grandezza che è la <math> c_i </math>, che è solidale all'attuatore scelto.

quindi ai valori <math> (x,y,z) </math>, incognite della sfera, sostituisco i relativi <math> ^{\left \{ A \right \}}Sf_i </math> ottengo una equazione di secondo grado in <math> c_i </math>. una delle due soluzioni dell'equazione è il legame tra <math> c_i </math> i=1..6 e i sei gradi di liberà dell'<math> {\left \{ EE \right \}}</math>.

Soluzioni Cinematica Inversa

le sei equazioni risolutive le trovate in File:LinaPod 6Dof r1.zip il software per gestirlo è Maxima un potente software di CAS (Computer Algebra System).

(sono nella sezione 5 sotto il nome della funzione:'soluzione_2_c_i(D,d,B,b,t_1,t_2,t_3,be,ga)' con i=1..6)

inoltre i conti fatti sono stati verificati con un CAD meccanico appurandone la coerenza.

6DOF o 5DOF

la scelta di creare una macchina a sei gradi di libertà (6DOF) è stata fatta pensata per rendere la macchia più semplice e simmetrica possibile.

per il tipo di lavorazione (stampa 3D) sono sufficenti cinque gradi di libertà per fare le lavorazioni.

Prospettive

spero che qualcuno serva questo lavoro per continuare lo studio e la realizzazione di macchine che gestiscano i sei gradi di libertà, in particolare si deve sviluppare il software per generare il percorso utensie (CAM software) [1] e l'elettronica di controllo che deve gestire 3 assi in più.