Firmware/Linear Acceleration

WIP: This is a Work In Progress

Physics of Motion

Velocity

A change in position is motion. The speed of that change is velocity. Velocity is the first derivative of position with respect to time. That's why velocity is measured as distance/time. V=dx/dt

Acceleration

A change in velocity is acceleration. Acceleration is the first derivative of velocity with respect to time. That's why acceleration is measured as distance/(time^2). A=dv/dt

Jerk

[ Note: this is not the "jerk" value commonly used to smooth out movements on some firmware in the community. ]

A change in acceleration is called "jerk". Jerk is the first derivative of acceleration, the 2nd derivative of velocity, and the third derivative of position. Jerk is measured as distance/(time^3). J=da/dt

Path Planning

Path planning is the process of determining how to move the axes to achieve a desired motion or displacement. Higher speeds are possible on stepper motors only through acceleration. The math required to determine stepper times to effect an accelerated motion involves calculus. Some of this calculus is not algebraically solvable.

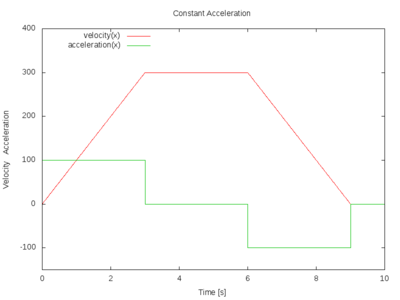
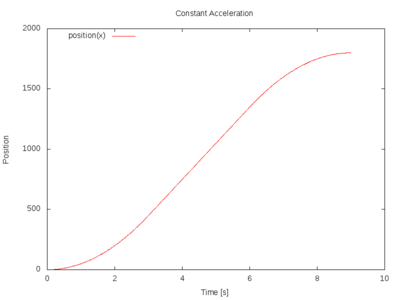
Constant Acceleration

To move the print head correctly, we need to convert acceleration into velocity and velocity into position. Most firmware uses Constant_Acceleration). It is mostly good enough and the math used to turn acceleration and time into step timing estimates is simpler than that for variable acceleration planning.

Linear Acceleration

Velocity planning using linear acceleration requires slightly more complicated math to calculate the stepper timings. It is difficult or impossible to do the required math in real-time on most microcontrollers. There are methods to estimate the correct values, but the precise answer can be attained only analytically (trial and error). There are small errors which accumulate over time when estimations are used, but these can be corrected by determining the error during the movement and compensating for it.

<image showing linear trapezoidal acceleration and resulting velocity>

Here I present a method to achieve linear acceleration through a constantly refined estimation. What we want to do is to calculate the precise time of the next step of the stepper motor. We cannot calculate this value exactly, but we can estimate it, and we can measure when the real moment has passed.

<image showing estimated step time, true "ideal" step time, and measured error>

By estimating the next step time in advance, we get a measure of how much slack time is available to perform other tasks (processing g-code, reading thermistors, etc.). When the moment nears when a step needs to occur, we can look to see how much movement should have occurred so far. If it is enough to warrant a step, we can step. If it does not yet add up to a whole step, we can delay a little more and check back later. In fact, if we are really clever, we can determine how _much_ later we should check back, thus refining our estimate. Doing this sort of estimate refinement well can reduce the number of re-estimations we need to do.

<image showing estimated step time, estimated refinements, ideal step times, and real step times; also show piece-wise "area under the curve" measurement of each step>

In effect we perform the analytical calculus needed to determine how movement _should have_ occurred. If we do this often enough (Teacup Firmware uses a 2ms "background" timer for such tasks) we can adjust our velocity in near-real time to match a planned velocity path.

<image of constant acceleration and resulting velocity curve>

Curved Acceleration

The velocity path can be calculated on the fly as the piece-wise integration of some linear acceleration value, or it can be a pre-calculated linear velocity ramp, the integral of some constant acceleration value. But it can also be a linear approximation to some complex curve.

I am using it to approximate the velocity curve discussed in this paper (PDF) on exponential velocity planning. The main goal of this complex exponential acceleration planning is to produce smooth, continuous movements free of sudden acceleration changes (jerk). But there are some other interesting ideas to come out of this paper, too.

Infinite jerk

The problem with constant acceleration is infinite jerk. When you go from zero acceleration to max acceleration in zero time, you experience infinite jerk. It's not really infinite, because real physics gets in the way. But the software tries to impart infinite jerk, and the hardware does its best to comply.

Any time the acceleration curve is discontinuous (broken), there is an instantaneous (theoretically infinite) jerk imparted on the machine. This causes stress on the machine parts and over time can damage or wear out the hardware prematurely.

One way to solve this is to use a trapezoidal acceleration profile. In this profile acceleration is a continuous function, but its slope, aka "Jerk", is not. But Jerk is then constant, at least, and not infinite. The resulting velocity profile is smoothed out, and our position plan is even smoother.

<image of constant Jerk, trapezoidal acceleration, smooth velocity>

Exponential velocity planning

A paper presented in the IEEE in 2013[1] proposed an exponential velocity planning method. Read the paper for all the details. In a nutshell it suggests that a function can be chosen whose first, second, and third derivatives are all continuous curves. Using this function to plan movements therefore leads to smooth acceleration and jerk profiles as well. Detailed analysis of these functions was done and simplified methods to normalize the curve to fit various velocity, acceleration and jerk limits were discovered. Most of the complex math can be solved in advance so the method can be implemented in real time.

Displacement time

A novel idea I learned from this paper involved displacement time, Td. Td is the amount of time required to make a move. It's quite simple, really. But the authors of this paper discovered some interesting ways to play with this notion. Here's a simplified description:

Td is the amount of time required to make a move at some max velocity, Vmax. The shortest possible Td occurs when we complete our entire move at Vmax. We can't really do that because we have to deal with acceleration and momentum and the real world. But let's decide what Td is as a lower bound of our movement time.

• Vmax: movement velocity, expressed as distance/time.
• dx: Distance to move
• Td = dx / Vmax = distance / (distance / time) = time

As an example, if we wish to move 40mm and our velocity Vmax is 120mm/sec, then our ideal travel time (displacement time) is given as:

 Td = 40mm / (120mm / sec) = (40 / 120) sec = 1/3 sec

This is all very basic. But what happens when we add in acceleration? Things get so complicated. There is often much math involved. You will find mechatronics papers discussing the 7 movement phases of an accelerated motion, and the 21 equations that must be solved to determine the movement in each phase. Whole books are written on this.

But what I learned from this paper is that it is much simpler than this if we rely on symmetrical acceleration and deceleration, which we do. Here's the interesting part.

<image> This a graph of the "ideal" motion where all travel occurs at Vmax. It's a rectangle. Rectangles are easy, right? Side * side = area. Area in this case is 40mm^2. The "y" side is 120mm/sec. So how big is the "x" side (time)? 40mm / 120mm/sec = 1/3 sec, or 0.3333 seconds.

<image> What happens when we introduce acceleration? In the simple case of constant acceleration, we have a trapezoidal velocity. That means our velocity curve forms a triangle for the acceleration at the start of the move and another triangle for our deceleration at the end of our movement. In the middle we managed to reach Vmax for some period of time. That's called the cruising period, or Tc. Note that it's important to be able to calculate Tc in advance so we know when to begin our deceleration. If we begin decelerating too soon, we will not complete our move. If we begin too late, we will not be able to stop our move at the desired position. We must begin decelerating at _exactly_ the right moment.

<image trapezoidal velocity with shaded areas for Ts, Tc and Ts> Since we didn't get to go top speed the whole time, our motion time is longer than 1/3 of a second. How long it is depends on how steep our velocity is (acceleration). But notice that the area under the curve is the same. The area under the curve is our position change, our dx.

Consider three areas of our curve. Ts = startup time when we were accelerating Tc = cruise time during which we travel at Vmax Te = end time when we have completed our travel

What about the deceleration time? It turns out that because our deceleration and acceleration profiles are symmetrical that it is simple to calculate when to begin decelerating. It is Te - Ts.

How do we calculate Te? Te = Td + Ts.

So Td is actually our deceleration start time.

  Te = Td + Ts
  Te - Ts = (Td + Ts) - Ts 
  Te - Ts = Td

This works because our triangles are identical; the area of a triangle is 1/2 height * base. So, two triangles add up to our ideal travel time graph again.

We can make this relationship work for more complicated profiles which do not use triangles. The paper glosses over that a bit, but it makes use of it. Look there if you want to understand it from the primary source. But the basic idea is so simple. We create our deceleration profile as the inverse of our acceleration profile, no matter what they look like. To make this inverse, we simply subtract our acceleration profile from Vmax when we want to begin decelerating. Where do we want to begin decelerating? At Td = Te - Ts. And Td = dx / Vmax.

<image of complex velocity profile accelerating and decelerating>

Linear approximation

Discussion of linear approximation methods to map velocity or acceleration profiles.

Movement joining

Introducing positional error to keep velocity up.