Open hardware fast high resolution LASER
This article article describes a transparent polygon laser diode scanner. The article aims to make room for an open-hardware version.
Contents
Description
Commercial laser diode sources can provide light at wavelengths down to 375 nm. The maximum power for single mode commercial laser diodes of 405 nm and 375 nm is 350 mW (SLD3237VF) and 70 mW (NDU4116) respectively. This optical power output is critical for a high waver throughput in printed circuit board manufacturing. A lot of energy can also be useful for photo-polymerization printers. The critical energy dosage for 60 volume percent silicon oxide and 55 volume percent alumina is 60-400 mJ/cm2 and 500-3300mJ/cm2, see Halloran. As a result, it can be advantageous to combine several laser diodes to solidify a single layer. This article tries to present a cost-effective illumination system which is able to combine the power of several laser diodes. Light can have up to two polarizations, so up to two single mode laser diodes can be combined into one bundle. In the figures shown to outline the chosen solution, a single laser diode is focused directly via an aspherical lens. This results into an elliptical spot. A spherical spot can be achieved by first collimating the laser diode with an aspherical lens and then circularizing the bundle with an anamorphic prism pair. The bundle can hereafter be focused with for example an achromatic doublet. Imaging with a single lens element has been chosen as it is cheaper. The polygon can be made by polishing the sides of a quartz sheet. In reflective polygon scanners the polygon is hit with a large collimated spot so it can be focused to a very small spot by the F-theta lens. In transparent polygon scanners, the beam is already converging and the spot can be smaller; which keeps the disk light. The bearing of the scanner can be created with a ball bearing, an air bearing or a self-sustaining air bearing. In the current solution, a self-sustaining air bearing is chosen as they have the size of a credit card, are cheap and readily available. After focusing, the laser diode bundle is displaced by rotating a transparent plate. The transparent plate is formed by the opposite sides of a regular convex polygon with an even number of sides. The illumination head is moved perpendicular to the scanning direction, so the substrate can be solidified. Another solution would be to move the substrate relative to the now static illumination head. This could be desirable as self-sustaining air bearings with a high speed rotating disk are best kept in a static position.
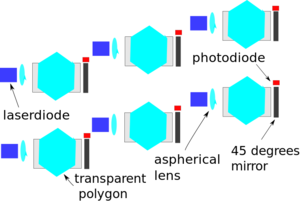
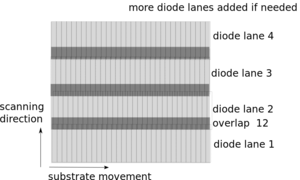
In figure 1, a possible embodiment is shown. In figure 1, a polygon cell consists out of three transparent polygons. Two polygon cells are shown in figure 1. More polygon cells can be added to the light engine if the exposure area needs to be enlarged.The transparent polygons project lines which must overlap partially, if the illumination unit or substrate is moved orthogonal to the illumination direction on the substrate. The embodiment shown can be used to solidify six lanes. The overlap between lanes is required to allow for correction of alignment errors in the optical design. Four lanes and three overlaps are shown in figure 2. The alignment errors can be detected by a camera which is moved under the illumination unit in the setup. Projection should be done directly on the CCD chip of the camera. A gray filter can be placed on the camera to protect the CCD chip.Search Report
There are several other laser diode polygon scanners which can be used to combine the power of multiple laser diodes. KLEO Halbleitertechnik which was partly owned by Zeiss and later sold to Manz sells the Speedlight 2D. The Speedlight 2D is a system which uses 9 polygons and 288 laser diodes to solidify a substrate with a width of 650 mm. The reflective polygon has 32 facets and rotates at a speed of 50.000 rotations per minute, see patent US8314921B2. The Netherlands Organization for Applied Scientific Research (TNO) has done a lot of research in transparent polygon scanners. It developed a system which is similar to that of Kleo AG but uses a transparent instead of a reflective polygon, for details see patent application WO 2015/160252 A1. The transparent polygon scanner proposed in this article is different than that from TNO in that it uses a single and not multiple optical bundles per transparent polygon. In addition, the rotation axes of the the proposed system are orthogonal and not co-planar with the substrate. The first polygon scanner in additive manufacturing was used by the Institute of Physical and Chemical Research (RIKEN) in 1997. In 2013, Envisiontec filed a patent US20130001834 A1 for a reflective polygon scanner in additive manufacturing to protect its Scan, Spin and Selective Photocure (3SP) technology. Other patents of relevance are; US6897888B2 (interleaving of scan patterns), US6731320B1 (varying the duration of pixels to compensate for scan velocity variations). This might be mitigated by shifting information to other pixel and not extending or shrinking pixels in time. Older transparent polygon scanners are; US5216534 (Read-write head for an optical tape recorder), US5815242A (Wide field scanning opthamoscope), US5428467 (Transmissive polygonal optical scanning of illumination for light valve video projector).
Business Case
Competitor Analysis
The large area photo-polymerization market and printed circuit board (PCB) market are seen as the commercially most interesting markets. High end large area photo-polymerization machines or PCB machines tend to be closed source and start at 250K euro’s. In the photo-polymerization market competing machines are the PromakerL7000D (Prodways), ProX 950 (3D Systems) and XEDE 3SP(Envisiontec). Formlabs has been omitted as it uses a collimated bundle, i.e. the laser diode is not focused. The number of pixels offered by DMD printers like the Rapidshape or Carbon 3D is seen to be too small even with a 4K DMD. In the PCB market competing machines are the Nuvogo Fine 10 (Orbotech), Speedlight 2D (Manz) and the Ledia 3WL (Ucamco). The resolution requirements of the PCB markets and additive manufacturing (AM) are estimated at 15 micrometers and 50 micrometers respectively. It is therefore thought that market entry can best be achieved via the AM market and later the PCB market.
Competing Technologies
The following technologies can be distinguished;
- Polygon scanner with F-theta lens and one laser bundle
- Used by: Envisiontec, Orbotech
- Limits: Three element F-theta lenses are expensive, telecentric systems are even more expensive and can, unlike transparent polygon scanner, not project outside the lens. For high-resolution systems, it can be beneficial to use a thick polygon, for a supplier see Lincoln Laser. An example calculation is given here. Transparent polygons can be thinner as the bundle is already focused.
- Reflective polygon scanner with multiple laser bundles
- Used by: Manz
- Limits: the polygon tilt angle is smaller than 45 degrees, most likely costs 1 million euro's
- Transparent polygon scanner with multiple laser bundles
- Used by: LDI Systems (defunct)
- Advantages: telecentric projection, system can project telecentric outside the lens, polygon tilt angle can be 45 degrees
- Limits: at best proof of concept, light engine in the order of 1K euro's per mm of projection
- DMD chip illuminated with LEDs
- Used by: Ucamco and Prodways
- Advantages: PCBs can be illuminated with multiple wavelengths which can be advantageous for PCB manufacturing, DMD is able to project several pixels at once, laser scanners are not able and therefore in the photo-polymerized lines are visible.
- Limits: multiple beamers can be placed adjacent to each other but this expensive, as a result Prodways translates the beamer and illuminates a 45 degrees mirror, if the mirror is illuminated with laser diodes this can result into multiple-slit interference.
- Galvanometer scanner with Nd:YAG LASER
- Used by: 3D Systems, Materialise
- Limits: low power and frequency of Nd:YAG laser, due to inertia galvanometer scanners are slower than polygon scanners
The Grating Light Valve, sold by companies like Silicon Light Machines, is typically used for mask-less lithography with 2.5 micrometer features. Too few applications of the MEMS scanner developed by Fraunhofer were known to take it into consideration. The femtosecond laser, which can be used in two-photon polymerization to focus light in space and time and trigger a non-linear reaction, was thought be too expensive for large-area photo-polymerization.
Competing Light Sources
The following light sources have been considered;
- Light-Emitting Diode (LED)
- Used by: Ucamco and Prodways
- Wavelengths: 405, 395, 385, 374, 365
- Frequency: set by other element in the optical path, e.g. the refresh rate of the DMD chip
- Power:<4 watt
- Price: 5 euro's per LED
- Note: LEDs offer less contrast and depth of field than laser diodes but can be combined as they do not produce coherent light. Texas Instrument seems to have a monopoly on DMD chips. Projection systems are sold by other vendors; for example, the LUXBEAM Lithography System sold by Visitech for >10k euro's. DMD chips can handle less optical power at shorter wavelengths. For wavelengths below 405 nm, the power limit is currently 4 W per chip DLP9000UV.
- Laser Diode (LD)
- Used by: Manz, Envisiontec
- Wavelengths: 405, 395, 375 nm
- Frequency: 50 MHZ
- Price: 40 euro's at 405 nm, 3870 euro's at 375 nm
- Power: 0.4 W at 405 nm, 70 mW at 375 nm
- Cooling: SLD3237VF can operate at 80 degrees.
- Diode-Pumped Solid State Laser (DPSSL)
- Used by: Orbotech
- Wavelength: 355 nm
- Frequency: 80 MHZ
- Power: 24 W
- Price: 190k euro's (only laser, you also need a chiller and a power supply)
- Vendor: Coherent
- Sizes: LASER 305 x 200 x 1100 mm, power supply 482 x 177 x 505 mm,
- Nd:YAG LASER
- Used by: 3D systems and Materialise
- Wavelength: 355 nm
- Power: 1 W
- Frequency: < 1MHZ
Proof of Concept
The target system should be able to produce 3D printed parts with a cross-sectional size of at least 200x200 <math>mm^2</math> at a resolution of 50 micrometers with a wavelength of 405 nm. The light engine of this system should cost at maximum 30K euro's. To proof this is feasible, it has to be shown that a single transparent polygon can be made for less than 300 euro's. A CCD camera is used to ensure the spot can be kept in position and the spot size is less than 50 micrometers.
Bill of Materials
- Quartz optical window, 2 mm thick, square cross-section of 35x35 mm, 150 dollars (note disk must weigh less than 8 grams)
- Ricoh Aficio AF-1027/270, 20 dollars (also used in the OpenExposer)
- iC-HG 200 MHz Laser Switch development board, 100 dollars (IChaus)
- PIN photodiode with blue enhanced sensitivity, BPW 34 B (Osram)
- FPGA: XuLa 2-LX25, 119.00 dollars with StickIt! v-4, 19.95 dollars
- Computer: Raspberry 3, 16GB SDHC, 1 meter network cable, housing, 2A microusb power, 62 dollars
- Software: Ubuntu 16.04, Python 3.5 (libraries: FPGA Myhdl, Spot Detection OpenCV, Slicer VTK)
- CCD camera; open
- Grey Filter
- Laserdiode: BDR-209 0.9 W (no spec sheet, unofficial data), 40 dollars
- Laser diode socket: S038S, 3.42 euro
- ESD protection: Lasorb L44-683, 7 dollars
- Protective glasses (HEALTH RISK: Do not look directly or indirectly into UV405 0.5W laser use a CCD camera or paper)
Physics
In the following, an analytical description of the system is given. The section starts with a parameter definition. Hereafter, the following properties are discussed; polygon, spot and transparent parallel plate.
Parameter Definition
The polygon rotates about its center, i.e. the point inside the polygon that is equidistant from each vertex. The substrate moves under the polygon in a certain direction. The smallest angle between the illumination direction and the substrate movement direction is defined as the polygonal tilt angle.
- <math>\alpha</math> denotes the static polygonal tilt angle. In the proposed system, this is 90 degrees.
- <math>\alpha^'</math> denotes the polygonal while scanning (the polygon tilt angle is speed dependent)
- <math>I</math> is the angle of incidence of the optical beam on the transparent polygon
- <math>I_{max}</math> is the maximum angle of incidence used during illumination
- <math>f_{efl}</math> is the effective focal length of the lens used to focus the bundle
- T defines the thickness of the polygon, T is equal to 2r.
- r defines the inradius of the polygon
- a defines the polygon side length
- R defines the circumradius of the polygon
- v is the number of vertices of the polygon.
- n is the refractive index of the polygon, quartz is used with a refractive index of 1.47
- d is the diameter of the aspherical lens
- <math>\lambda</math> defines the center wavelength of the laser diode beam
Polygon
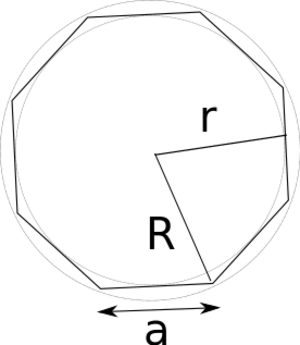
In figure 3, a regular convex polygon is shown with the following parameters; r is the inradius, R is the polygon circumradius and a is the polygon side length. In figure 3, the number of vertices, v, is equal to 8. Earlier, we defined 2r to be equal to T. The number of facets of the polygon has to be even for opposing planes to be parallel. If the number of facets is uneven, there will be an edge crossing during illumination which makes it unsuited for scanning.
- <math>a=T\cdot tan(\pi/v)</math>
- <math>R=\dfrac{a}{2 \cdot sin(\pi/v)}</math>
- The interior angle of a simple polygon with v vertices is <math>180-360/v</math> degrees.
For an octagon, <math>I_{max}</math> cannot be larger than 67.5 degrees.
Spot
Light emerges from a small optical window from the laserdiode and as a result diverges. There are several ways to focus the diverging beam. The choice is a trade-off between spot quality and cost. Two possibilities are discussed; (1) an aspherical lens and (2) with achromatic doublet after collimation with an aspherical lens and circulation with an anamorphic prism pair.
Lens Alignment
The lens alignment is determined by the optical magnification of the whole system. The emission point typicaly has a size of 0.5 micrometers by 1 micrometers. The size can be measured via the Fraunhofer diffraction pattern. The emission point accuracy is assumed to be +/- 80 micrometers. This was estimated from similar laser diodes. For a 50 micrometers spot, the aspheric lens has to be placed at an accuracy of 3 micrometers (simulation should be added). The magnification is 50. The aspheric lens can be purchased mounted with a M9 thread and screwed into position with a screw driver.
Rayleigh length
The spot is defined to be in focus in twice the Rayleigh length; <math>z_r=\dfrac{2 \pi w_0^2}{M^2 \lambda}</math>. <math>M^2</math> is called the beam quality factor. Most collimated single TE mode laser diode beams have <math>M^2</math> of 1.1 to 1.2, source Sun, Haiyin.
Spot size
The spot size of a collimated and circulated bundle focussed by an achromatic doublet is <math>w_0=\dfrac{4\lambda}{\pi}\dfrac{f_{efl}}{D}</math>, where D is the diameter of the collimated bundle. The spot distance is <math>f_{efl}</math> from the achromatic doublet.
The spot distance of a laserdiode directly projected by an aspheric lens is given by the thin lens equation; <math>\dfrac{1}{f_{efl}}=\dfrac{1}{s_1}+\dfrac{1}{s_2}</math>. <math>S_1</math> denotes the distance between the laser diode and the aspheric lens. <math>S_2</math> denotes the separation between the aspheric lens and the spot. The magnification,M, is given by <math>M \approx -\dfrac{s_2}{s_1}=\dfrac{f}{f-s_1}</math>. As the emission point is not square, the spot will be elliptical.
The smallest spot which can be formed is given by the Airy disk. <math>w_0=1.22\dfrac{s_2 \lambda}{D}</math>. Here D is the width of the collimated beam or divergent beam at the lens.
Transparent Parallel Plate
The properties of a parallel plate are described by Smith and Wyant. The most important properties of a parallel plate are summarized in this section. Typically, a parallel plate is used to transversely shift a collimated bundle. For a converging beam, a parallel plate also gives a longitudinal focus point displacement towards the source and optical aberrations. The optical aberrations increase if I is increased. Via an analytical calculation it is ensured that the Strehl ratio is above the Rayleigh limit at <math>I_{max}</math>.
Displacement
- longitudinal displacement <math>=\dfrac{n-1}{n}T</math>
- transversal displacement <math>=T sin I(1-\sqrt{\dfrac{1-sin^2 I}{n^2-sin^2 I}})</math>
- The spot speed can be derived by differentiation the transversal displacement with respect to I. The speed at the center is smaller than the speed at the edges of a projected line. As a result, the amplitude at the center should be smaller and is ideally corrected for by the laser diode driver by varying the pulse frequency or current.
Seidel Aberrations
The f-number or <math>f_\#</math> equals <math>\dfrac{f_{efl}}{D}</math>. A transparent plate does not have a Petzval field curvature aberration. As a result, the projection of the transparent polygon is telecentric. The other aberrations are:
- spherical wavefront abberation <math>=-\dfrac{T}{f_\#^4}\dfrac{n^2-1}{128n^3}</math>
- coma <math>=-\dfrac{TU}{f_\#^3}\dfrac{n^2-1}{16n^3}cos\theta</math>
- astigmatism <math>=-\dfrac{TU}{f_\#^2}\dfrac{n^2-1}{8n^2}cos^2\theta</math>
The wavefront aberrations can be used to calculate the Strehl ratio. If the Strehl ratio gets below a limit during illumination, the aberrations will become dominant and the system will not image properly. As a result, it must be ensured via calculation that the Strehl ratio is larger than some acceptable limit, e.g. the Rayleigh limit of 0.71. Systems with a spot size close to 10 micrometers are possible. The main challenge is the placement of the optical components.
Simulation
The calculation can be verified with an open optical ray tracing and lens design framework, such as the Python library made by Dr. Jordens named Rayopt.