EndMatching
The RepRapHostSoftware does end matching automatically in order to organize a slice into coherent 2D geometry. It's part of the process of converting from a 3D object in STL file format to into movement instructions for your RepRap in standard G-Code file format.
Organizing a slice into coherent 2D geometry
After slicing (ZSlicing), the program has a collection of line segments, which (as we shall see) are commonly less well-behaved than this. But the picture gives the idea. Note that the coordinates of the ends in general won't match precisely because of rounding errors an the like.
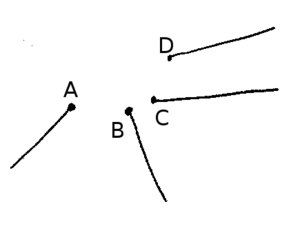
You might imagine that the obvious thing to do would be to join up the ends by matching each to its nearest other endpoint. But - as often - the obvious thing to do is the wrong thing to do. The principal problem is that the idea "nearest other endpoint" is not reciprocal: A can have B as its nearest point, whereas B's nearest is C. How would you choose to join these in pairs? And if you say join A to B and C to D, precisely what geometrical rule are you following?
In fact, as long as A, B, C, and D are all closer than the resolution of the machine, it doesn't matter what pairing choice you make as long as you avoid the one out of the three possibilities where the pairing lines cross (which would give a figure-of-eight polygon). But it is essential that such small-scale arbitrary decisions don't accumulate in pathological cases to a scale larger than the resolution of the machine.
The RepRap code in org.reprap.geometry.polygons.STLSlice solves this by recursively dividing the line end points in a quad tree. The surrounding rectangle is easy to compute - it is just the extremal points in x and y. Indeed, this rectangle is tracked and constructed as the points are being added by the slicing code.
The terminating rule for the recursion is that a quad contains either no endpoints, or it contains two belonging to different line segments. There is a further termination rule, which is that there is a small lower limit to the length of a quad diagonal. This is needed for those occasions where more than two end points coincide to stop an infinite recursion. More on this in a minute.
The quad tree is not even, as you can see on the right; the quads are not similar. The coordinate for dividing a quad in x is decided by sorting a list of all the x coordinates of the line segment ends in the quad, finding the median value, and looking either side of that for the nearest gap in the list greater than a certain size. Half way across that gap is the chosen x coordinate for the division. The same is done for y. In the cases where the coordinates are too densely packed to find a gap "greater than a certain size" an arbitrary gap somewhere near the middle of the list is chosen.
As the quad tree is divided, line segment endpoints have to be classified as to whether they are in a quad or not. The rectangle representing each quad is slightly expanded when this is done to make sure that no endpoints fall down the cracks. This is slightly inefficient, but much more robust. And everything gets automatically sorted out further down the division anyway.
It is now straightforward to join up the ends: each pair in each non-empty quad are joined.
Note that, though it seems complicated, this algorithm is almost certainly much faster than a simple search for nearest neighbours (which, as we just saw, won't work anyway). Unless you want to go to the trouble of constructing something like a Voronoi diagram of the endpoints to find those neighbours, such a search would probably take a time that is O(N2), where N is the number of segments. Though I haven't proved it, the quad tree should, I think, be O(N log(N)). A quad tree is a spatial equivalent of sorting in one dimension, so one would expect that O(N log(N)) would be the best that one can do.
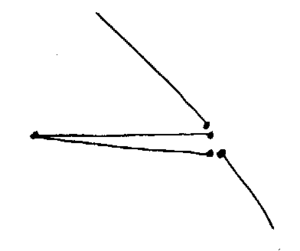
A common problem is that shown on the right, where the cluster of four points that I have shown as being distinct actually coincide. This is caused by dud triangles in the original STL file that either shouldn't be there, or that should be in a different place. The spike created is obviously spurious, and couldn't exist in physical reality. The four coincident points cause the recursive quad division to hit its small-quad-diagonal limit. The code then checks for this special case, and deletes the points forming the spike, leaving just two line segments to join up.
Where is the source code to implement end matching and spike removal?
I expected to see "end matching" implemented in the "AllSTLsToBuild.java" source file. In particular, I expected "end matching" to be implemented in either
- (a) the
recursiveSetEdges()method after it converts STL 3D triangles to edges, or - (b) the
slice()method somewhere between the point it callsrecursiveSetEdges()and thensimpleCull(), or - (c) the
simpleCull()method just before it converts edges to polygons.
Alas, I don't see it there ...
simplify polygons
We now have one or more polygons, but a final problem remains. STL is very profligate with triangles, and generates zillions of the things, even for flat surfaces. This means that chains of line segments in the polygons we've generated should probably be single straight lines.
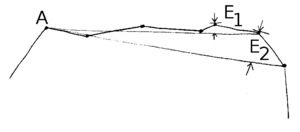
The RepRap code filters these as follows. Starting at point A on a polygon, it repeatedly constructs a line to the next point but one, the next point but two, and so on. For each line it examines the points in between that are not on it and finds their distance E from the line. When it finds a value of E (like E2) that is bigger than an acceptable small number, it backtracks (to the immediately-previous point that generated E1) and replaces all the little line segments in between with that one long segment.
This way the polygon is simplified, and the RepRap machine doesn't end up plotting loads of short lines when one long one would do.
Point A is found by running the algorithm from an arbitrary start point and choosing the first corner the filter finds from that start.
The polygons are now ready to be passed to the CSG evaluation functions.
-- Main.AdrianBowyer - 25 Feb 2008
This process of simplifying polygons is implemented in the simplify() method of the
"RrPolygon.java" source code.